hi,
in der global übung wirde gesagt das lim a_n = lim a_n+1 gilt für n->oo.
Weiter soll aber lim[ a_n+1 / a_n ] = 1 nich gelten. Warum denn das nich? kann mir das jmd erklärn?
mfg chris
[AfI] folgen grenzwert
17 Beiträge
• Seite 1 von 2 • 1, 2
Re: folgen grenzwert
chrisblablub hat geschrieben:Weiter soll aber lim[ a_n+1 / a_n ] = 1 nich gelten. Warum denn das nich?
Ich schätze mal du verwechselst
-

fw - Beiträge: 1356
- Registriert: 17.05.06 19:37
- Studiengang: Informatik (Dipl.)
- Studiert seit: fertig
- Anwendungsfach: Mathe
Re: folgen grenzwert
chrisblablub hat geschrieben:hi,
in der global übung wirde gesagt das lim a_n = lim a_n+1 gilt für n->oo.
Weiter soll aber lim[ a_n+1 / a_n ] = 1 nich gelten. Warum denn das nich? kann mir das jmd erklärn?
mfg chris
ganz einfach (vollkommen informal, aber hoffentlich verständlich
lim a_n ist quasi das element a_oo, also ein element von "möglichst weit hinten" in deiner folge, bzw formal: der grenzwert der folge
lim a_n+1 ist quasi das element a_{oo+1} - aber logischerweise gilt: unendlich + 1 = unendlich (was bringt es mir, wenn ich nach dem ende noch eins dazu tu, wenn ich das ende sowieso nie erreiche?)
aber, zum thema lim[ a_n+1 / a_n ] - stell dir vor, du hast eine folge, in der die zahl in jedem schritt halbiert wird (1/(2^n)) - nun suchst du dir zwei beliebige aufeinander folgende elemente. du wirst feststellen, dass a_{n+1} / a_n immer != 1 ist. wenn du nun also eine unendliche folge dieser brüche betrachtest, und davon ein element von "möglichst weit hinten", wird das niemals 1 sein. also lim[ a_n+1 / a_n ]!=1
mfg
mirko
- mirko
- Beiträge: 1032
- Registriert: 22.10.06 18:33
- Studiert seit: WS 12/13
mirko hat geschrieben:user hat geschrieben:Das ist grober Unfug, mirko.
dass es informal ist, hab ich ja selbst schon gesagt - ich wollte mehr eine intuition geben... - inwiefern es unfug ist, musst du mir aber erklären...
Betrachte eine konstante Folge. Deine Aussage ist pulverisiert (nicht nur für diesen Fall übrigens).
Ich bin mir ziemlich sicher, dass fw Recht hat.
"Alle Menschen sind klug;
die einen vorher, die anderen nachher" (Voltaire)
die einen vorher, die anderen nachher" (Voltaire)
-

Muffi - Beiträge: 392
- Registriert: 05.07.06 11:14
- Wohnort: Aachen
- Studiengang: Informatik (Dipl.)
- Studiert seit: SS 07
- Anwendungsfach: Mathe
Re: folgen grenzwert
chrisblablub hat geschrieben:Weiter soll aber lim[ a_n+1 / a_n ] = 1 nich gelten.
Muffi hat geschrieben:Betrachte eine konstante Folge.
hä? entweder hab ich wirklich etwas komplett nicht verstanden, oder deine aussage passt nicht wirklich zum thread-titel. für eine konstante folge gilt doch "lim[ a_n+1 / a_n ] = 1" oder nicht?
unabhängig davon, weiß ich nicht, in wie weit das meine aussage kaputt machen sollte:
mirko hat geschrieben:lim a_n ist quasi das element a_oo, also ein element von "möglichst weit hinten" in deiner folge, bzw formal: der grenzwert der folge
lim a_n+1 ist quasi das element a_{oo+1} - aber logischerweise gilt: unendlich + 1 = unendlich (was bringt es mir, wenn ich nach dem ende noch eins dazu tu, wenn ich das ende sowieso nie erreiche?)
bis hierhin sehe ich keinen widerspruch...
mirko hat geschrieben:aber, zum thema lim[ a_n+1 / a_n ] - stell dir vor, du hast eine folge, in der die zahl in jedem schritt halbiert wird (1/(2^n)) - nun suchst du dir zwei beliebige aufeinander folgende elemente. du wirst feststellen, dass a_{n+1} / a_n immer != 1 ist. wenn du nun also eine unendliche folge dieser brüche betrachtest, und davon ein element von "möglichst weit hinten", wird das niemals 1 sein. also lim[ a_n+1 / a_n ]!=1
hier beziehe ich mich auf das beispiel der folge "1/(2^n)" - dass du da ein anderes beispiel bringst, für die meine aussage nicht gilt, ist schön, aber es ging doch darum, zu zeigen, dass das komplement meiner aussage keine allgemeingültigkeit besitzt. dass es in ausnahmefällen gilt, ist ja schön, aber irrelevant...
mfg
mirko
- mirko
- Beiträge: 1032
- Registriert: 22.10.06 18:33
- Studiert seit: WS 12/13
a_n ist das n-te glied der folge
a_n+1 ist somit das (n+1)-te glied der folge
(ich nehme mal an, gemeint ist a_{n+1} und nicht {a_n}+1)...
die folge an sich ändert sich also nicht, man greift nur auf ein element aus der folge zu...
a_n+1 ist somit das (n+1)-te glied der folge
(ich nehme mal an, gemeint ist a_{n+1} und nicht {a_n}+1)...
die folge an sich ändert sich also nicht, man greift nur auf ein element aus der folge zu...
- mirko
- Beiträge: 1032
- Registriert: 22.10.06 18:33
- Studiert seit: WS 12/13
DEserrt hat geschrieben:Hä, jetzt bin ich verwirrt. Heißt lim an+1 nicht, dass die Folge um ein Glied nach rechts verschoben ist. Ich bei der Folge 1/n also nicht mehr 1, 1/2, 1/3..., sondern 1/2, 1/3,.... habe?
Wieso unendlich + 1?
Jo, heißt es.
Aber 1/n und 1/(n+1) konvergieren ja beide gegen 0, und bei jeder anderen Folge konvergieren an und an+1 auch beide gegen dasselbe, also lim an = lim an+1 und damit, wie fw sagte lim an / lim an+1 = 1 und das immer (bei konvergenten Folgen).
Jedoch gilt dies für lim an/an+1 nicht, wie mirkos Beispiel zeigt und wieso das Unfug sein sollte, ist mir nicht klar^^
Bei DEserrts Bsp wäre das lim (1/n) / (1/(n+1)) = lim (n+1)/n = 1, bei mirkos Bsp jedoch lim (1/(2^n)) / (1/(2^n+1)) = lim (2^(n+1)) / (2^n) = lim 2 = 2
Es kann also durchaus auch 1 rauskommen, muss es aber nicht
Also hat chris das wahrscheinlich verwechselt, so wie fw gesagt hatte...
Was macht man, wenn man ein ungelöstes Problem hat?
Man gibt ihm einfach einen Namen!
(copyright Hawi)
Man gibt ihm einfach einen Namen!
(copyright Hawi)
- MaoDelinSc
- Beiträge: 296
- Registriert: 07.12.07 10:28
- Wohnort: Aachen
- Studiengang: Informatik (B.Sc.)
- Studiert seit: WS 09/10
- Anwendungsfach: Medizin
MaoDelinSc hat geschrieben:DEserrt hat geschrieben:Hä, jetzt bin ich verwirrt. Heißt lim an+1 nicht, dass die Folge um ein Glied nach rechts verschoben ist. Ich bei der Folge 1/n also nicht mehr 1, 1/2, 1/3..., sondern 1/2, 1/3,.... habe?
Wieso unendlich + 1?
Jo, heißt es.
dann musst du aber konsequenterweise auch sagen, dass sich die welt unter'm auto wegdreht
prinzipiell kannst du dir das natürlich auch so vorstellen... - die frage ist dann nur, was du bei a_{n-1} machst...
MaoDelinSc hat geschrieben:Aber 1/n und 1/(n+1) konvergieren ja beide gegen 0, und bei jeder anderen Folge konvergieren an und an+1 auch beide gegen dasselbe, also lim an = lim an+1 und damit, wie fw sagte lim an / lim an+1 = 1 und das immer (bei konvergenten Folgen).
Jedoch gilt dies für lim an/an+1 nicht, wie mirkos Beispiel zeigt und wieso das Unfug sein sollte, ist mir nicht klar^^
Bei DEserrts Bsp wäre das lim (1/n) / (1/(n+1)) = lim (n+1)/n = 1, bei mirkos Bsp jedoch lim (1/(2^n)) / (1/(2^n+1)) = lim (2^(n+1)) / (2^n) = lim 2 = 2
Es kann also durchaus auch 1 rauskommen, muss es aber nicht
dem kann ich soweit uneingeschränkt zustimmen...
- mirko
- Beiträge: 1032
- Registriert: 22.10.06 18:33
- Studiert seit: WS 12/13
Bitte benutzt LaTeX, das macht die Sache viiiieeel lesbarer.
Ich bin mir gar nicht sicher, was überhaupt der Ursprung dieses Threads war.
Es soll gelten:
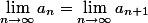
Jedoch soll nicht (immer) gelten:
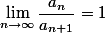
Bei Wikipedia ist dazu zu finden, dass gilt:
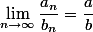 , sofern a und b die Grenzwerte dieser beiden Folgen sind (und existieren und
, sofern a und b die Grenzwerte dieser beiden Folgen sind (und existieren und 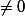 sind!).
sind!).
Da ich mir ja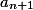 einfach als
einfach als 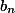 deklarieren kann, ist das kein Problem.
deklarieren kann, ist das kein Problem.
Folgt man diesem Link findet man noch folgendes. Und hier bin ich mir unsicher, ob das denn so in der Allgemeinheit stimmt:
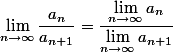
Denn wenn das so stimmen würde, wäre MartinLs Beispiel falsch. Ist es aber nicht.
^{n+1} \frac{1}{n+1}}{(-1)^n \frac{1}{n}} = \lim_{n\to\infty} - \frac{n}{n+1} = -1)
Die obige Rechenregel kann man nicht anwenden, da der Grenzwert 0 ist.
Also kann man schonmal davon ausgehen, dass nicht zwingend 1 rauskommen muss.
Das Problem ist hier, dass die Teilfolgen einmal von unten und einmal von oben gegen 0 konvergieren. Dadurch kommt es zur -1.
Ich habe jetzt mal folgendes gemacht:
^n\frac{1}{n}+1) konvergiert nicht mehr gegen 0, sondern gegen 1. Damit wird die Rechenregel wieder anwendbar.
konvergiert nicht mehr gegen 0, sondern gegen 1. Damit wird die Rechenregel wieder anwendbar.
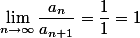
So weit so gut, rechne ich jedoch per Hand:
^{n+1} \frac{1}{n+1}+1}{(-1)^n \frac{1}{n}+1} = \dots= -1)
Wer findet meinen Fehler, oder ist die Rechenregel Murks?
Ich bin mir gar nicht sicher, was überhaupt der Ursprung dieses Threads war.
Es soll gelten:
Jedoch soll nicht (immer) gelten:
Bei Wikipedia ist dazu zu finden, dass gilt:
Da ich mir ja
Folgt man diesem Link findet man noch folgendes. Und hier bin ich mir unsicher, ob das denn so in der Allgemeinheit stimmt:
Denn wenn das so stimmen würde, wäre MartinLs Beispiel falsch. Ist es aber nicht.
Die obige Rechenregel kann man nicht anwenden, da der Grenzwert 0 ist.
Also kann man schonmal davon ausgehen, dass nicht zwingend 1 rauskommen muss.
Das Problem ist hier, dass die Teilfolgen einmal von unten und einmal von oben gegen 0 konvergieren. Dadurch kommt es zur -1.
Ich habe jetzt mal folgendes gemacht:
So weit so gut, rechne ich jedoch per Hand:
Wer findet meinen Fehler, oder ist die Rechenregel Murks?
Klein-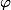 macht auch Mist....
macht auch Mist....
- DominikP
- Beiträge: 242
- Registriert: 12.11.07 21:29
- Wohnort: Aachen, vorher Korschenbroich bei MG
- Studiengang: Informatik (M.Sc.)
- Studiert seit: WS 07/08
- Anwendungsfach: BWL
DominikP hat geschrieben:Bei Wikipedia ist dazu zu finden, dass gilt:, sofern a und b die Grenzwerte dieser beiden Folgen sind (und existieren und
sind!).
Da ich mir jaeinfach als
deklarieren kann, ist das kein Problem.
das nützt dir zumindest dann nichts, wenn die folge gegen 0 konvergiert... - ich frage mich gerade, ob
DominikP hat geschrieben:Folgt man diesem Link findet man noch folgendes. Und hier bin ich mir unsicher, ob das denn so in der Allgemeinheit stimmt:
das kann zumindest schonmal nicht gelten, wenn
DominikP hat geschrieben:
Wer findet meinen Fehler, oder ist die Rechenregel Murks?
für n=50 und n=49 bekommt mein taschenrechner für das zwischen den sternen jedenfalls werte nahe +1 raus - spricht also vieles für einen rechenfehler bei deinen 3 punkten (oder einen tippfehler meinerseits)
- mirko
- Beiträge: 1032
- Registriert: 22.10.06 18:33
- Studiert seit: WS 12/13
Natürlich gilt das was du oben geschrieben hast.
Die Grenzwertsätze liefern einen für den Fall, dass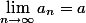 und
und 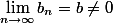 , dass
, dass 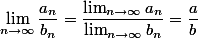 und somit auch, dass für ein solches
und somit auch, dass für ein solches 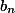 gilt dass
gilt dass 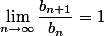
Die stehen auch so irgendwo im AfI Script da wo es auch entsprechungen für Addition und Multiplikation konvergenter Folgen gibt.
Was dein Beispiel angeht ...
^{n+1} \frac{1}{n+1}}^{\to 0}+1}{\underbrace{(-1)^n \frac{1}{n}}_{\to 0}+1} = 1)
Die Grenzwertsätze liefern einen für den Fall, dass
Die stehen auch so irgendwo im AfI Script da wo es auch entsprechungen für Addition und Multiplikation konvergenter Folgen gibt.
Was dein Beispiel angeht ...
Zuletzt geändert von MartinL am 07.02.09 15:09, insgesamt 1-mal geändert.
- MartinL
- Beiträge: 531
- Registriert: 23.01.07 20:48
- Studiert seit: WS 06/07
- Anwendungsfach: Mathe
17 Beiträge
• Seite 1 von 2 • 1, 2
